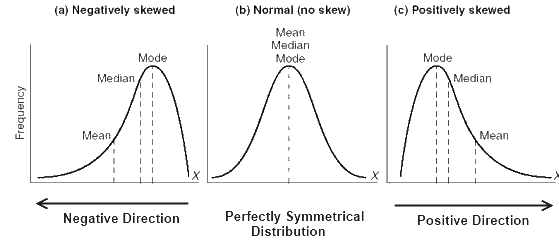
In statistics, a central tendency (or measure of central tendency) is a central or typical value for a probability distribution. It may also be called a center or location of the distribution. Colloquially, measures of central tendency are often called averages. The term central tendency dates from the late 1920s.
The most common measures of central tendency are the arithmetic mean, the median and the mode.
Arithmetic Mean
The arithmetic mean is the most common measure of central tendency. It is simply the sum of the numbers divided by the number of numbers. The symbol “μ” is used for the mean of a population. The symbol “M” is used for the mean of a sample. The formula for μ is shown below:
μ = ΣX/N
where ΣX is the sum of all the numbers in the population and
N is the number of numbers in the population.
The formula for M is essentially identical:
M = ΣX/N
where ΣX is the sum of all the numbers in the sample and
N is the number of numbers in the sample.
As an example, the mean of the numbers 1, 2, 3, 6, 8 is 20/5 = 4 regardless of whether the numbers constitute the entire population or just a sample from the population.
MEDIAN
Median is the value which occupies the middle position when all the observations are arranged in an ascending/descending order. It divides the frequency distribution exactly into two halves. Fifty percent of observations in a distribution have scores at or below the median. Hence median is the 50th percentile.[2] Median is also known as ‘positional average’.
It is easy to calculate the median. If the number of observations are odd, then (n + 1)/2th observation (in the ordered set) is the median. When the total number of observations are even, it is given by the mean of n/2th and (n/2 + 1)th observation.
Advantages
It is easy to compute and comprehend.
It is not distorted by outliers/skewed data.
It can be determined for ratio, interval, and ordinal scale.
Disadvantages
It does not take into account the precise value of each observation and hence does not use all information available in the data.
Unlike mean, median is not amenable to further mathematical calculation and hence is not used in many statistical tests.
If we pool the observations of two groups, median of the pooled group cannot be expressed in terms of the individual medians of the pooled groups.
MODE
Mode is defined as the value that occurs most frequently in the data. Some data sets do not have a mode because each value occurs only once. On the other hand, some data sets can have more than one mode. This happens when the data set has two or more values of equal frequency which is greater than that of any other value. Mode is rarely used as a summary statistic except to describe a bimodal distribution. In a bimodal distribution, the taller peak is called the major mode and the shorter one is the minor mode.
Advantages
It is the only measure of central tendency that can be used for data measured in a nominal scale.
It can be calculated easily.
Disadvantages
It is not used in statistical analysis as it is not algebraically defined and the fluctuation in the frequency of observation is more when the sample size is small.
